洛谷P1955 《[NOI2015]程序自动分析》

五月 12, 2018 5541

第一道NOI的题目

洛谷 P1955 题解

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3…代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入输出格式

输入格式：

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若e=0，则该约束条件为xi≠xj；

输出格式：

输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

输入输出样例

输入 #1

1
2
3
4
5
6
7
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出 #1

1
2
NO
YES

输入 #2

1
2
3
4
5
6
7
8
9
10
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出 #2

1
2
YES
NO

数据范围（图片来自洛谷）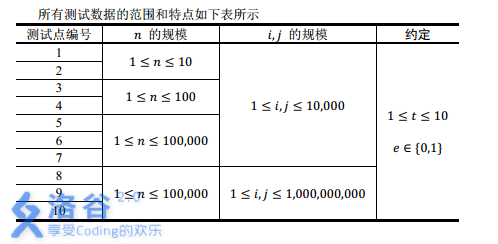
data

解题思路

把题目中的「x1=x2」看做x1和x2在同一个集合里，「x1≠x2」看做x1和x2不在同一个集合里……

好了，显而易见这是道并查集的题目

读懂了题目，下手就很简单了

这里要注意：
「x1≠x2」是无法进行的操作（因为你不能强制他们不在同一个集合里！若非要实现，就又要维护一个数组），把它看成查询操作。

而且「x1=x2」类似的操作要先做，「x1≠x2」类似的操作要最后做（因为后者对集合没有影响，它是一个查询操作）

1
2
3
4
5
6
7
如果你遇到了类似这样的数据：
...
1 2 0
1 2 1
...
那么根据我们的思路， 「1 2 0」是一个查询操作，对集合没有影响，那么就相当于少了一个操作！
必须要先进行「x1=x2」类似的合并操作，再做「x1≠x2」类似的查询操作

代码实现

90分代码 评测记录（未离散化）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;

const int MAXN = 100000 + 10;

int U[MAXN], n, t;
int e[MAXN], e0[MAXN], x[MAXN], y[MAXN];

/* 快读 */
inline int getInt() {
	int s = 0, x = 1;
	char ch = getchar();
	while (ch > '9' || ch < '0') {
		if (ch == '-') x = -x;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		s = s * 10 + ch - '0';
		ch = getchar();
	}
	return s * x;
}

inline int Find(int x) {
	if (U[x] == x) return x;
	return U[x] = Find(U[x]);
}

inline void Union(int x, int y) {
	x = Find(x), y = Find(y);
	if (x == y) return;
	U[x] = y;
	return;
}

bool Main() {
	n = getInt();
	for (int i = 0; i < MAXN; ++i) {
		U[i] = i;
	}
	memset(e, 0, sizeof(e));
	memset(x, 0, sizeof(x));
	memset(y, 0, sizeof(y));
	for (int i = 1; i <= n; ++i) {
		x[i] = getInt(), y[i] = getInt(), e[i] = getInt();
	}
	int j = 1;
    // 第一次做 「x1=y1」的合并操作
	for (int i = 1; i <= n; ++i) {
		int fe = e[i], fx = x[i], fy = y[i];
		if (fe == 1) Union(fx, fy);
	}
   //  第二次做 「x1≠y1」的查询操作
	for (int i = 1; i <= n; ++i) {
		int fe = e[i], fx = x[i], fy = y[i];
		if (fe == 0) {
			if(Find(fx) == Find(fy)) return false;
		}
	}
	
	return true;
}

int main() {
	ios::sync_with_stdio(false);
	t = getInt();
	for (int i = 0; i < t; ++i){
		if (Main()) puts("YES");
		else puts("NO");
	}
}

离散化

简介

——引自百度百科

1
2
3
4
5
离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。
通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。例如：
原数据：1,999,100000,15；处理后：1,3,4,2；
原数据：{100,200}，{20,50000}，{1,400}；
处理后：{3,4}，{2,6}，{1,5}；

对一堆数据进行离散化，

  1. 先排序 [ 推荐 std::sort() ]（针对有序序列进行离散化）
  2. 删除重复元素（节省空间）
  3. 对数据进行索引（最终目的）

而其中我们要用到STL提供的pair来储存变量。pair提供一个包含两个数据成员的结构体模板，可以快速访问其中的元素，就像一个压缩包一样（

代码实现

AC代码 评测记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#define Pair pair<ll,ll> 
using namespace std;

typedef long long int ll;

const int MAXN = 600000 + 10;

int U[MAXN], n, t;
int e[MAXN], x[MAXN], y[MAXN];

Pair p[MAXN];

inline int getInt() {
    int s = 0, x = 1;
    char ch = getchar();
    while (ch > '9' || ch < '0') {
        if (ch == '-') x = -x;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        s = s * 10 + ch - '0';
        ch = getchar();
    }
    return s * x;
}

inline int Find(int x) {
    if (U[x] == x) return x;
    return U[x] = Find(U[x]);
}

inline void Union(int x, int y) {
    x = Find(x), y = Find(y);
    U[x] = y;
    return;
}

bool stlCmp(Pair x, Pair y) {
    return (x.first > y.first);
}

void Disc(Pair a[], int A[]) {
    int tot = 0;
    sort(a + 1, a + n*2 + 1, stlCmp);
    for (int i = 1; i <= n*2; ++i) {
        if (i == 1 || a[i].first != a[i-1].first) tot++;
        A[a[i].second] = tot;
    } 
} 

bool Main() {
    n = getInt();
    for (int i = 0; i < 500010; ++i) {
        U[i] = i;
    }
    memset(e, 0, sizeof(e));
    memset(x, 0, sizeof(x));
    memset(y, 0, sizeof(y));
    memset(p, 0, sizeof(p));
    for (int i = 1; i <= n; ++i) {
        int ax = getInt(), ay = getInt(), ae = getInt();
        e[i] = ae;
        p[i] = make_pair(ax, i);
        p[i + n] = make_pair(ay, i+n);
    }
    Disc(p, x);
    for (int i = 1; i <= n; ++i) y[i] = x[n + i];
    for (int i = 1; i <= n; ++i) {
        int fe = e[i], fx = x[i], fy = y[i];
        if (fe == 1) Union(fx, fy);
    }
    for (int i = 1; i <= n; ++i) {
        int fe = e[i], fx = x[i], fy = y[i];
        if (fe == 0) {
            if(Find(fx) == Find(fy)) return false;
        }
    }
    
    return true;
}

int main() {
    ios::sync_with_stdio(false);
    t = getInt();
    for (int i = 0; i < t; ++i){
        if (Main()) puts("YES");
        else puts("NO");
    }
}