欧拉图学习笔记

一月 18, 2019 4559

从一个点出发走一走

约定

  1. 定义 (A,B) 表示从 A \rightarrow B 的一条边（若无特别说明，即为无向边）
  2. 定义 (A,B) \rightarrow (C,D) 表示从 A \rightarrow D ，经过 (A,B), (C,D) 两条边的路径
  3. 定义「孤立点」表示一个度为 0 的点
  4. 定义「奇顶点」表示一个度数为奇数的点
  5. 定义对于有向图 G ，将所有的有向边替换为无向边得到图 G 的基图，若图 G 的基图是连通的，则称图 G 是「弱连通图」。
  6. Stack_a 表示标号为 a 的栈。
  7. 用 Stack_x = a]b]c] 表示 Stack_x 的层级结构，其中 a 为栈顶， c 为栈底。
  8. \text{Foo} \rightarrow \text{Bar} 表示 \text{Foo} 里的元素 \text{Bar} （表特指）

定义

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。
如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。
具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。

——百度百科

通俗地说，

对于一个图的某条路径，如果能从一个点出发将这个图的所有边都不重复地走一遍，那么这条路径就被称为欧拉路；对于一个图的某条路径，如果能从一个点出发将这个图的所有边都不重复地走一遍并回到起点，那么这条路径就被称为欧拉回路。

比如下图中的
MATHJAX-SSR-621
就是一条欧拉路。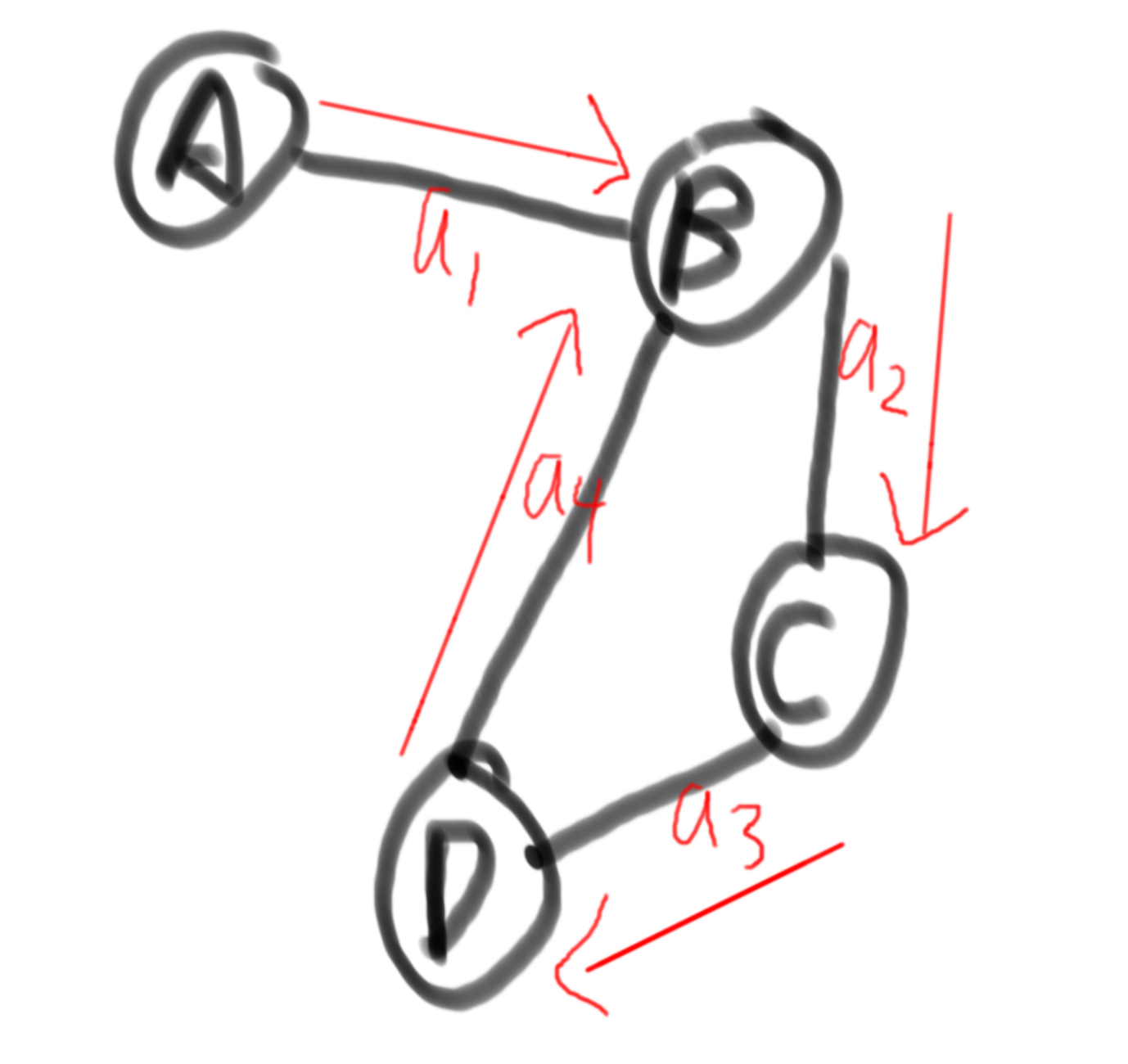
0

比如下图中的
MATHJAX-SSR-622
就是一条欧拉回路。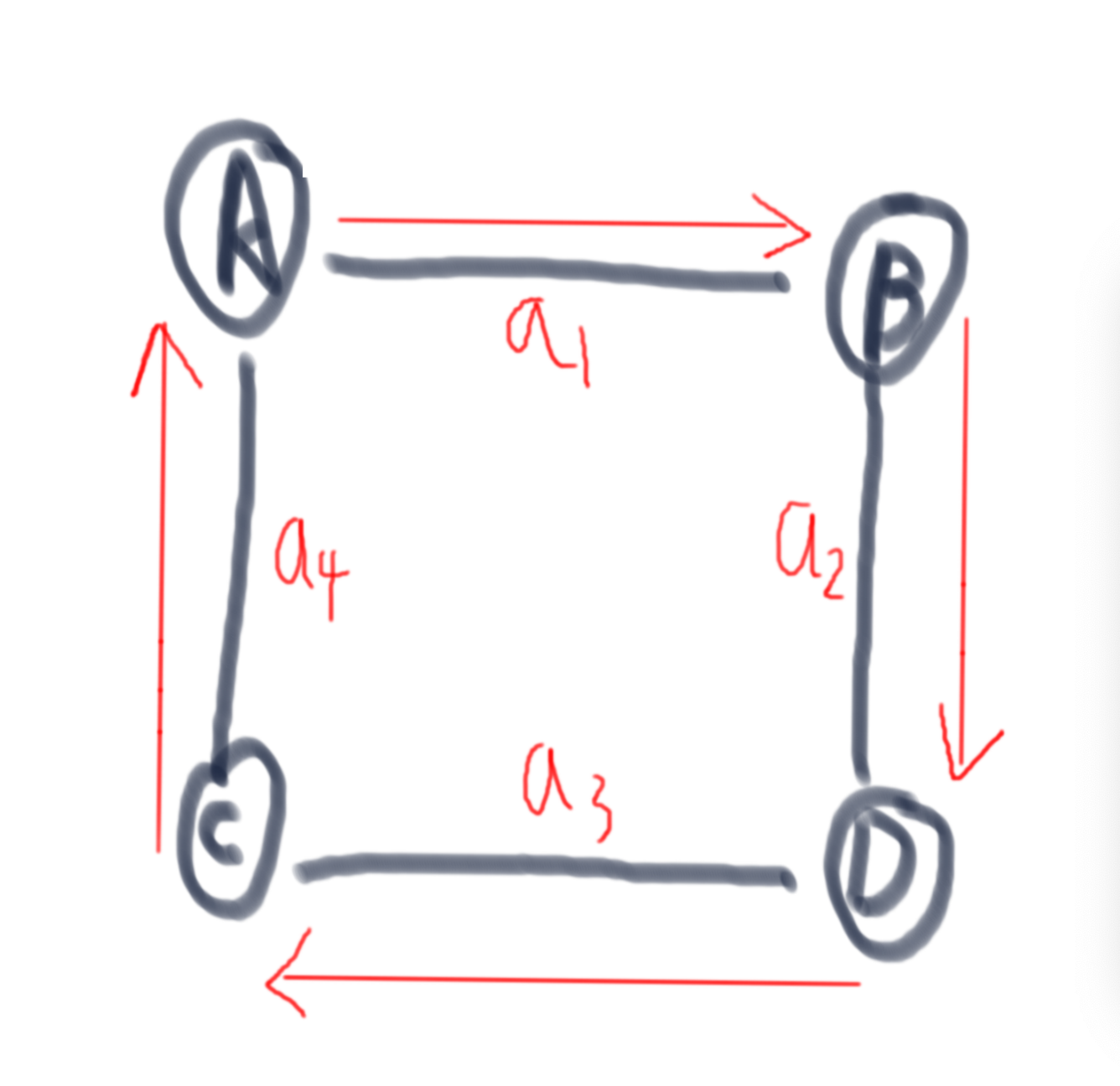
1

判定

无向图判定

  1. 无孤立点的无向图 G 为欧拉图，当且仅当图 G 连通且所有顶点的度都是偶数。

  2. 如果无向连通图有 2k 个奇顶点，则图 G 可以用 k 条路径将图 G 的每一条边经过 一次，且至少要使用 k 条路径。

  3. 无孤立点的无向图 G 为半欧拉图，当且仅当图 G 连通且 G 的奇顶点个数为 2 。 此时两个奇顶点分别为欧拉路径的起点和终点。

有向图判定

  1. 无孤立点的有向图 G 为欧拉图，当且仅当图 G 弱连通且所有顶点的入度等于出度。

  2. 对于连通有向图，所有顶点入度与出度差的绝对值之和为 2k ，则图 G 可以用 k 条路径将图 G 的每一条边经过一次，且至少要使用 k 条路径。

  3. 无孤立点的有向图 G 为半欧拉图，当且仅当图 G 弱连通，且恰有一个顶点 u 入度比出度小 1 ，一个顶点 v 入度比出度大 1 ，其余顶点入度等于出度。此时存在 u 作为起点， v 作为终点的欧拉路径。

求解

Hierholzier 算法

算法流程

任选一起点，沿任意未访问的边走到相邻节点，直至无路可走。此时必然回到起点形成了一个回路，此时图中仍有部分边未被访问。在退栈的时候找到仍有未访问边的点，从该点为起点求出另一个回路，将该回路与之前求出的回路拼接。如此反复，直至所有的边都被访问。

比如说我们有这样一张图：

2

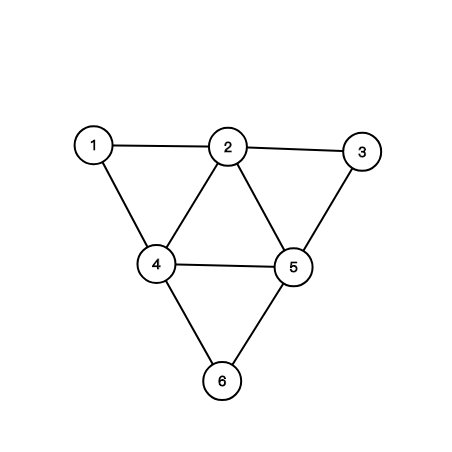
我们随便取一个点，比如说 1 ，把它加入一个栈。

Stack_1 = 1]

Path_1 = [\ ]

我们用 u 表示 Stack_1 \rightarrow Top
如果当前的 u 点已没有未访问的出边，就将 u 从 Stack_1 里弹出来，加入到 Path_1 的前端

重复上面的过程，直到 Stack_1 为空。

3
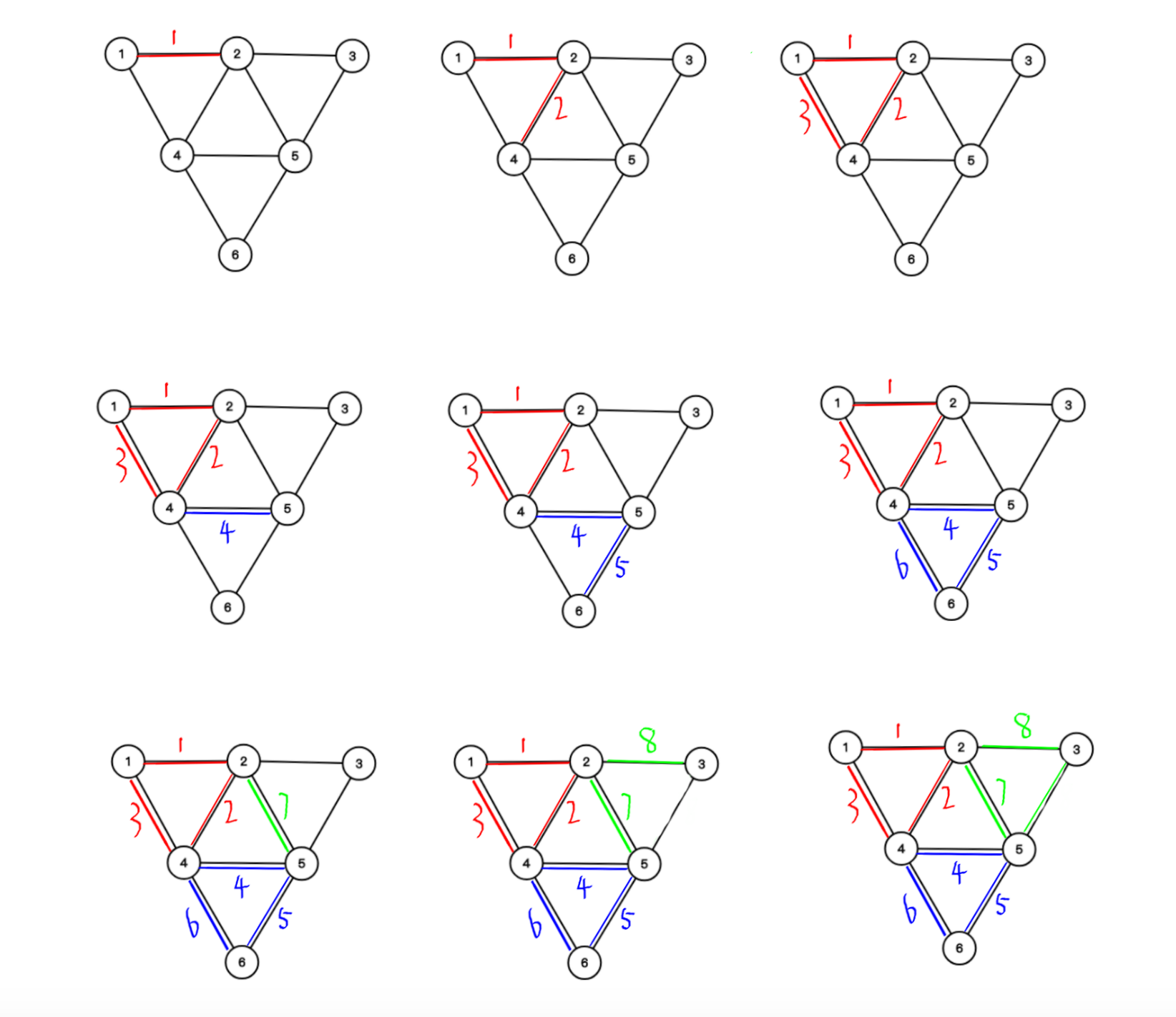
在这个过程中，
MATHJAX-SSR-625

Stack_1 = 4]2]1],\ Path_1 = [\ ]

Stack_1 = 1]4]2]1],\ Path_1 = [\ ]

Stack_1 = 5]4]2]1],\ Path_1 = [1]

Stack_1 = 6]5]4]2]1],\ Path_1 = [1]

Stack_1 = 4]6]5]4]2]1],\ Path_1 = [1]

Stack_1 = 2]5]4]2]1],\ Path_1 = [6,4,1]

Stack_1 = 3]2]5]4]2]1],\ Path_1 = [6,4,1]

Stack_1 = 5]3]2]5]4]2]1],\ Path_1 = [6,4,1]

所有的边都访问了，开始回溯存路径

Stack_1 = \ ],\ Path_1 = [1,2,4,5,2,3,6,4,1]

最终答案即为 Path_1

伪代码

假装自己写的是真正的 \LaTeX

⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯

\text{Algorithm 1: Hierholzer(s)}
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
1: \text{while s} 存在未被删除的无向边 (s,t)\ \text{do}
2:     删除无向边 (s,t)
3:      \text{Hierholzer(t)}
4: \text{End while}
5: cnt \leftarrow cnt + 1
6: Path[cnt] \leftarrow s
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯

代码实现

真正的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const int MAXN_M = 10000;

int G[MAXN_M][MAXN_M], ans[MAXN_M], cnt;

void Hierholzer(int s) {
    for (int t = __MIN_NODE; t <= __MAX_NODE; ++t) {
        // 预防数据中不出现标号为 1 的节点的情况
        // __MIN_NODE 指数据中标号最小的节点的标号
        // __MAX_NODE 同上
        if (G[s][t]) {
            // 使用邻接矩阵存图，更加易懂
            --G[s][t];
            --G[t][s];
            Hierholzer(t);
        }
    }
    ans[++cnt] = s;
}

Fluery 算法

挖坑待填

例题

洛谷 P2731 模板题

题解将会在不久后上传

其他事项

参考资料

  1. IOI2018 中国国家候选队论文集
  2. 洛谷 P2731 题解