Trie 树学习笔记

三月 02, 2019 3207

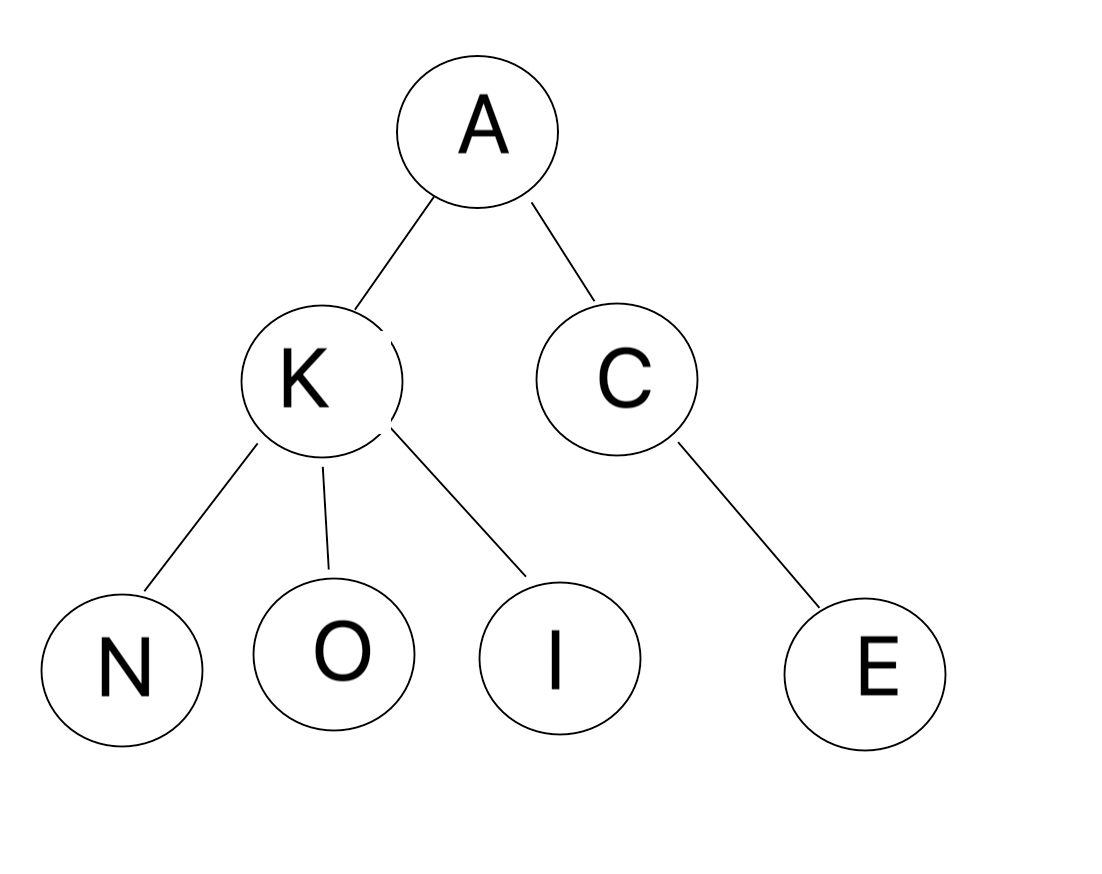
很简单的树形字符串结构

简介

在计算机科学中，Trie，又称字典树、单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

——百度百科

简单地说，Trie 树就是以字符串的字母为结构建立起来的一棵多根树
画出来大概是这样的

其中，这棵树有这些字符串

1
2
3
4
5
6
7
A
AK
AKN
AKO
AKI
AC
ACE

操作

都很简单。

插入操作

给你一个字符串，要求把这个字符串插入到树中

首先指定树根为0，当前位置为树根
枚举字符串的每个字符，看一下当前字符在当前深度有没有，有的话就直接把「当前位置」切换为这个字符所处的位置，没有的话就往里插入这个字符再切换

建议配合代码理解

查询操作

这里以查询是否被查询过为例

对于每一个字符，记一下以它为结尾的字符串是否被查询过
还是像插入一样切换当前位置，如果中间某一字符在那个深度没有，就直接返回字符串不存在
切换到字符串最后一个字符之后，看一下刚才记的那个变量是否为真即可

也还是建议配合代码理解

例题

这里以洛谷 P2580 于是他错误的点名开始了为例

题目大意

就是给你一堆字符串和一堆询问
对于每个询问，输出是否存在这个字符串
如果存在，输出它有没有被询问过

解题思路

本来这是一道std::map的模板题
但是我们是来学 Trie 的
那么当然要用 Trie 做啊（逃

代码实现

也是上面那一题的代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <iostream>
#include <cstring>
#include <string>

#define FILE_IN(__fname) freopen(__fname, "r", stdin)
#define FILE_OUT(__fname) freopen(__fname, "w", stdout)
#define IMPROVE_IO() std::ios::sync_with_stdio(false)

using std::cin;
using std::cout;
using std::endl;

const int MAXN = 10000 + 10;
struct Trie{
    // 日常封装
    struct Node {
        int size;
        int linkson[26 + 1];
        // 直接用它来记子节点的位置，类似于链表
        
        bool rep;
        
        Node() {
            size = 0;
            rep = false;
            memset(linkson, 0, sizeof linkson);
        }
    } tree[MAXN];
    
    int cnt;
    
    Trie() { cnt = 0; }
    
    void Insert(const char *s, int length) {
        // 插入
        int pos = 0; // pos = root
        for (int i = 0; i < length; ++i) {
            int ins = s[i] - 'a';
            if (tree[pos].linkson[ins] == 0) {
                // insert
                tree[pos].linkson[ins] = ++cnt;
                ++tree[pos].size;
            }
            pos = tree[pos].linkson[ins];
            // 前面提到的切换位置
        }
    }
    // 返回值就0, 1, 2，用不着 int
    short Find(const char *s, int length) {
        int pos = 0; // pos = root
        for (int i = 0; i < length; ++i) {
            int que = s[i] - 'a';
            if (tree[pos].linkson[que] == 0) return 2; 
            // 没找到这个名字
            pos = tree[pos].linkson[que];
            // 这里也是和上边插入一模一样
        }
        if (tree[pos].rep) return 1;
        // 重复点名
        tree[pos].rep = true;
        return 0;
        // 炉石传说真好玩（逃
    }
} T;

int n, m;


int main() {
    IMPROVE_IO();
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        std::string s;
        cin >> s;
        T.Insert(s.c_str(), (int) s.size());
    }
    cin >> m;
    for (int i = 1; i <= m; ++i) {
        std::string s;
        cin >> s;
        switch(T.Find(s.c_str(), (int) s.size())) {
            case 0: {
                printf("OK\n");
                break;
            }
            case 1: {
                printf("REPEAT\n");
                break;
            }
            case 2: {
                printf("WRONG\n");
            }
        }
    }
    return 0;
}