洛谷P5018「NOIP2018普及组」《对称二叉树》

三月 30, 2019 4580

一个长得像暴力的正解

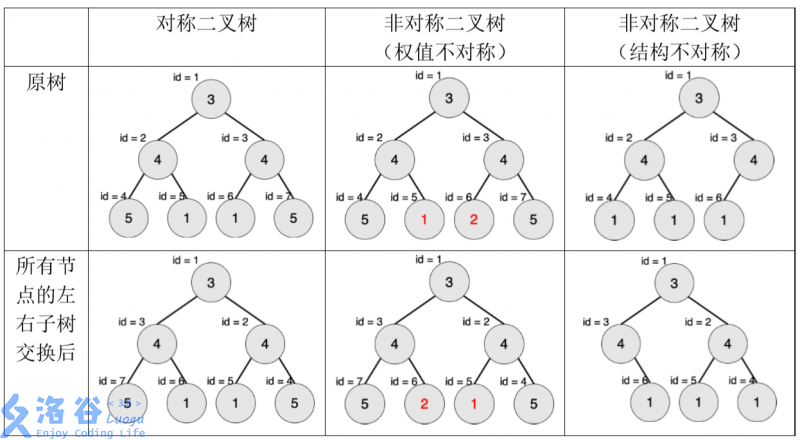
题目描述

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

  1. 二叉树；
  2. 将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

下图中节点内的数字为权值，节点外的 id 表示节点编号。

1

现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数 最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点T 为子树根的一棵“子 树”指的是：节点 T 和它的全部后代节点构成的二叉树。

输入输出格式

输入格式

第一行一个正整数 n，表示给定的树的节点的数目，规定节点编号 1 \sim n ，其中节点 1 是树根。

第二行 n 个正整数，用一个空格分隔，第 i 个正整数 v_i ​ 代表节点 i 的权值。

接下来 n 行，每行两个正整数 l_i, r_i ，分别表示节点 i 的左右孩子的编号。如果不存在左 / 右孩子，则以 -1 表示。两个数之间用一个空格隔开。

输出格式

输出文件共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

输入输出样例

输入样例#1

1
2
3
4
2 
1 3 
2 -1 
-1 -1

输出样例#1

1
1

输入样例#2

1
2
3
4
5
6
7
8
9
10
11
12
10 
2 2 5 5 5 5 4 4 2 3 
9 10 
-1 -1 
-1 -1 
-1 -1 
-1 -1 
-1 2 
3 4 
5 6 
-1 -1 
7 8

输出样例#2

1
3

说明

【数据规模与约定】
共 25 个测试点。
v_i ≤ 1000 。
测试点 1 \sim 3, n ≤ 10 ，保证根结点的左子树的所有节点都没有右孩子，根结点的右 子树的所有节点都没有左孩子。
测试点 4 \sim 8, n ≤ 10 。
测试点 9 \sim 12, n ≤ 10^5 ，保证输入是一棵“满二叉树” 。
测试点 13 \sim 16, n ≤ 10^5 ，保证输入是一棵“完全二叉树”。
测试点 17 \sim 20, n ≤ 10^5 ，保证输入的树的点权均为 1。
测试点 21 \sim 25, n ≤ 10^6 。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 1。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为 h，且二叉树有 2h−1 个节点，这就是满二叉树。

完全二叉树：设二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大 个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

解析

场上没写这道题真是血亏
被T3折磨得心态爆炸 也没心情写这题了。。。

首先它求的是满足要求的最大子树的大小
那就先 DFS 一遍求出所有子树的大小

1
2
3
4
5
6
7
8
9
10
11
void DFS(int root = 1) {
    // nodes[root].treeSize 已经被赋值为1了
    if (nodes[root].leftChild != -1) {
        DFS(nodes[root].leftChild);
        nodes[root].treeSize += nodes[LC(root)].treeSize;
    }
    if (nodes[root].rightChild != -1) {
        DFS(nodes[root].rightChild);
        nodes[root].treeSize += nodes[RC(root)].treeSize;
    }
}

然后呢？

一个很暴力的想法，就是暴力枚举根节点，判断一下这棵子树是否对称，对称就更新答案

判断对称是很好写的，递归即可

1
2
3
4
5
6
7
8
9
10
bool CheckSymmetric(int n1, int n2) {
    if (n1 == -1 && n2 == -1) return true; // 叶子节点
    if (
        (n1 != -1 && n2 != -1) /* 判断是否有完整的节点 */
        && nodes[n1].data == nodes[n2].data /* 判断节点信息是否相同 */
        && CheckSymmetric(LC(n1), RC(n2)) /* 递归判断两边的节点 */
        && CheckSymmetric(LC(n2), RC(n1)) /* 递归判断中间的节点 */
    ) return true;
    return false; // 判断失败
}

「递归判断两边 / 中间的节点」，是这么回事

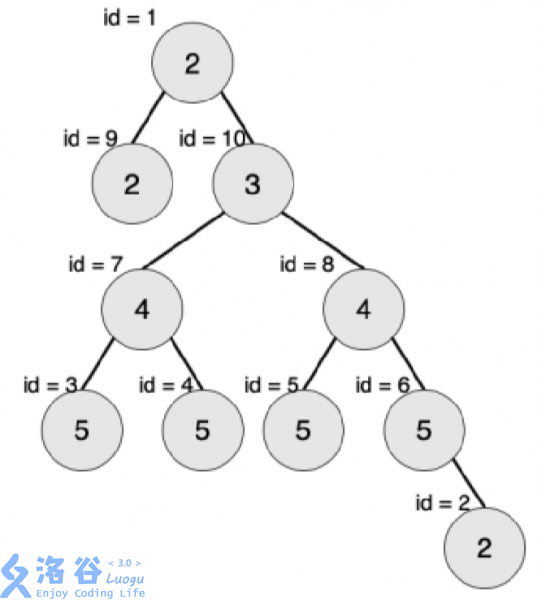
2

先假装节点id = 2不存在

在进行递归的时候，判断的是(id = 3, id = 6)和(id = 4, id = 5)
很明显判断对称的时候，要判断的就是这两个节点（和它们的子树）

代码分析完了，来算算这份暴力的复杂度

  • DFS 不用说
  • CheckSymmetric 的最坏情况是原树为完全二叉树，递归次数为树高（即 \log_2n ），又因为要暴力枚举一共 n 个点，所以复杂度为 O(n\log_2 n)

综上，程序复杂度为 O(n\log_2n) ，是能过的

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>

#define FILE_IN(__fname) freopen(__fname, "r", stdin)
#define FILE_OUT(__fname) freopen(__fname, "w", stdout)
#define IMPROVE_IO() std::ios::sync_with_stdio(false)
#define LC(x) ((nodes[x].leftChild))
#define RC(x) ((nodes[x].rightChild))

using std::cin;
using std::cout;
using std::endl;

const int MAXN = 1000000 + 10;

struct Node {
    int data;
    int leftChild;
    int rightChild;
    int treeSize;
    
    Node() : data(0), leftChild(0), rightChild(0), treeSize(1) {}
} nodes[MAXN];

int n;

void DFS(int root = 1) {
    if (nodes[root].leftChild != -1) {
        DFS(nodes[root].leftChild);
        nodes[root].treeSize += nodes[LC(root)].treeSize;
    }
    if (nodes[root].rightChild != -1) {
        DFS(nodes[root].rightChild);
        nodes[root].treeSize += nodes[RC(root)].treeSize;
    }
}

bool CheckSymmetric(int n1, int n2) {
    if (n1 == -1 && n2 == -1) return true; // leaf node
    if (
        (n1 != -1 && n2 != -1)
        && nodes[n1].data == nodes[n2].data
        && CheckSymmetric(LC(n1), RC(n2))
        && CheckSymmetric(LC(n2), RC(n1))
    ) return true;
    return false;
}

int main() {
    IMPROVE_IO();
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> nodes[i].data;
    }
    for (int i = 1; i <= n; ++i) {
        cin >> nodes[i].leftChild >> nodes[i].rightChild;
    }
    DFS();
    
    int ans = 0;
    // enumerate every subtree
    for (int i = 1; i <= n; ++i) {
        if (CheckSymmetric(LC(i), RC(i))) {
            ans = std::max(ans, nodes[i].treeSize);
        }
    }
    cout << ans << endl;
    return 0;
}