HDU2196《Computer》

八月 15, 2019 3768

利用树的直径的性质

Problem Description

A school bought the first computer some time ago(so this computer’s id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.

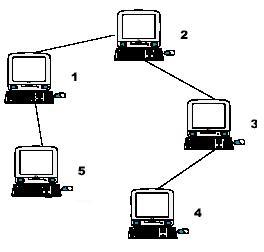
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

Input

Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

Output

For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

Sample Input

1
2
3
4
5
5
1 1
2 1
3 1
1 1

Sample Output

1
2
3
4
5
3
2
3
4
4

解析

首先有一个性质：在一棵树上，距离任意点最远的点一定是这棵树直径的一个端点

然后这题不就好做了吗

先以 1 为根求一遍直径，再分别以两个端点为根求一遍这个点到其他点的距离，取个最大值，输出即可，这个可以写一个DFS调用三遍

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
//
//  HDU2196.cpp
//  Title: Computer
//  Debugging
//
//  Created by HandwerSTD on 2019/8/15.
//  Copyright © 2019 HandwerSTD. All rights reserved.
//

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>

#define FILE_IN(__fname) freopen(__fname, "r", stdin)
#define FILE_OUT(__fname) freopen(__fname, "w", stdout)
#define rap(a,s,t,i) for (int a = s; a <= t; a += i)
#define basketball(a,t,s,i) for (int a = t; a > s; a -= i)
#define countdown(s) while (s --> 0)
#define IMPROVE_IO() std::ios::sync_with_stdio(false)

using std::cin;
using std::cout;
using std::endl;

typedef long long int lli;

int getint() { int x; scanf("%d", &x); return x; }
lli getll() { long long int x; scanf("%lld", &x); return x; }

const int MAXN = 10000 + 10;

struct Edge {
    int v, w;
    
    Edge(int v = 0, int w = 0) : v(v), w(w) {}
};

std::vector<Edge> head[MAXN];

int n, farthest;
lli maxdis;
lli f[MAXN];

inline void addEdge(int u, int v, int w) {
    head[u].push_back(Edge(v, w));
    head[v].push_back(Edge(u, w));
}

void DFS(int u, int fa, lli dis) {
    if (dis > maxdis) { maxdis = dis; farthest = u; }
    f[u] = std::max(f[u], dis);
    for (int i = 0, siz = (int) head[u].size(); i < siz; ++i) {
        int v = head[u][i].v, w = head[u][i].w;
        if (v == fa) continue;
        DFS(v, u, dis + w);
    }
}

void _main() {
    for (int i = 1; i <= n - 1; ++i) {
        int v = getint(); int w = getint();
        addEdge(i + 1, v, w);
    }
    int p1 = 0, p2 = 0;
    DFS(1, 0, 0);
    p1 = farthest;
    DFS(p1, 0, 0);
    // 以上这两遍DFS是在求树的直径
    // 第二遍DFS顺便更新了一下从某一个端点出发的答案
    p2 = farthest;
    DFS(p2, 0, 0);
    // 由于在每个点的最长路径可能到达两个端点
    // 所以要对两个端点分别更新一遍答案
    // 这一遍DFS是在更新从另一个端点出发的答案
    for (int i = 1; i <= n; ++i) printf("%lld\n", f[i]);
    memset(f, 0, sizeof f);
    for (int i = 1; i <= n; ++i) head[i].clear();
    n = maxdis = farthest = 0;
    return;
}

int main() {
    while (scanf("%d", &n) != EOF) _main();
    return 0;
}