洛谷P2158《[SDOI2008]仪仗队》

八月 18, 2019 4780

题目描述

作为体育委员，C君负责这次运动会仪仗队的训练。仪仗队是由学生组成的N * N的方阵，为了保证队伍在行进中整齐划一，C君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐(如下图)。

现在，C君希望你告诉他队伍整齐时能看到的学生人数。

输入格式

共一个数 N

输出格式

共一个数，即C君应看到的学生人数。

输入输出样例

输入 #1

1
4

输出 #1

1
9

说明/提示

【数据规模和约定】

对于 100% 的数据，1 ≤ N ≤ 40000

解析

来快乐推一推式子

首先考虑一下没有被看到的点长什么样
显然没有被看到的点 (x,y) 与原点的连线上一定有一点，记为 (\frac x t , \frac y t )

由于所有坐标都是整数，那么有

t \mid x, t \mid y \Leftrightarrow t \mid \gcd(x, y)

所以可以知道这个事情：
一个点 (x, y) 不可以被看到，等价于 \gcd(x, y) \neq 1 。
所以题目要求的就是所有的数对 (x,y) 的个数，满足 \gcd(x, y) = 1

分开考虑答案

首先是坐标形如 (0, y), (x, 0) 的这些点，也就是在 x 轴和 y 轴上的点，均只能看见一个 (0, 1),(1, 0) ，统计答案的时候就直接 + 2 就行了。

然后是在直线 y = x 上的点，也只能被看见一个 (1, 1) ，统计答案的时候再来个 + 1 。

剩下的点可以用两个 \sum 统计。
最后式子长这样（注意 \text{ans} 函数的参数值）：

\begin{align} \text{ans}(n + 1) = 3 + \sum_{x = 1}^{n} \sum_{y = 1}^{x - 1}[\gcd(x, y) = 1] + \sum_{x = 1}^{n} \sum_{y = x + 1}^{n}[\gcd(x, y) = 1] \end{align}

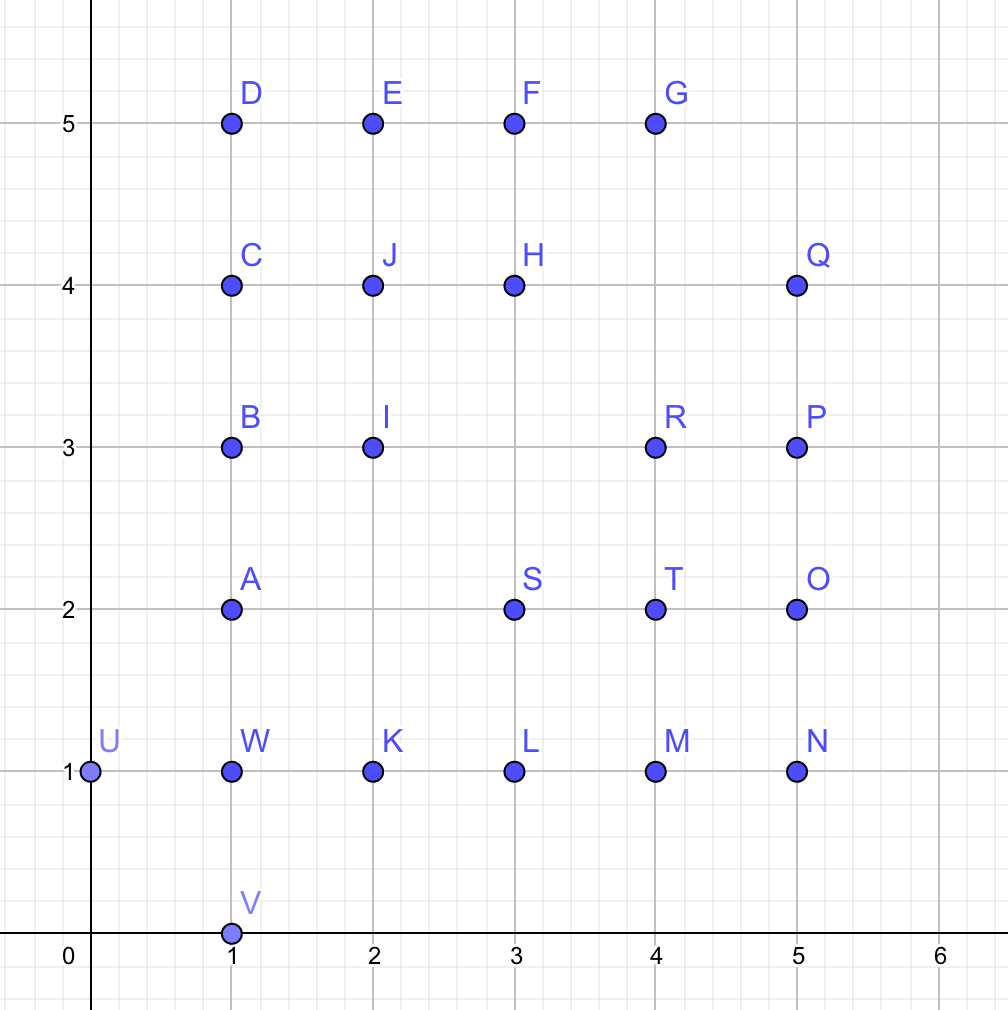
看一眼这张图：

可以发现，第一种情况对应的是点 U, V ，第二种情况对应的是 W ，两个 \sum 分别对应点 A \rightarrow J 和 K \rightarrow T 的能看见的点的数量。

还是不懂？ 手动模拟一下吧，看看它会统计哪些点
两个 \sum 相当于语句

1
2
3
4
5
6
7
8
ans = 0
for x = 1 to n do
	for y = 1 to x - 1 do
		ans = ans + (gcd(x,y) == 1)
for x = 1 to n do
	for y = x + 1 to n do
		ans = ans + (gcd(x,y) == 1)
ans = ans + 3

显然可以看到的点是关于直线 y = x 对称的，所以上面的式子又可以写成

\text{ans}(n + 1) = 3 + 2\sum_{x = 1}^{n} \sum_{y = 1}^{x - 1}[\gcd(x, y) = 1]

这个式子肯定跑不过去的。把这个式子化简一下

注意到一个很常见的积性函数

\varphi(x) = \sum_{i = 1}^{x}[\gcd(i, x) = 1]

代入原式！

\text{ans}(n + 1) = 3 + 2\sum_{x = 1}^{n} \sum_{y = 1}^{x - 1}[\gcd(x, y) = 1]
= 3 + 2\sum_{x = 1}^{n} (\sum_{y = 1}^{x}[\gcd(x, y) = 1] - [\gcd(x, x) = 1])
= 3 + 2\sum_{x = 1}^{n} (\varphi(x) - [\gcd(x, x) = 1])

好了，现在就有了一个可以 O(n) 计算的式子了！

（式子要分行写是因为我博客的 Math 引擎好像炸了。。。渲染不了多行，将就看吧/kk）

最后说个事， n = 1 的时候答案为 0 ，这个很显然吧，都没有学生了（

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
//
//  LuoguP2158.cpp
//  Title: [SDOI2008]仪仗队
//  Alternatives: BZOJ2190
//  Debugging
//
//  Created by HandwerSTD on 2019/8/18.
//  Copyright © 2019 HandwerSTD. All rights reserved.
//

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>

#define FILE_IN(__fname) freopen(__fname, "r", stdin)
#define FILE_OUT(__fname) freopen(__fname, "w", stdout)
#define rap(a,s,t,i) for (int a = s; a <= t; a += i)
#define basketball(a,t,s,i) for (int a = t; a > s; a -= i)
#define countdown(s) while (s --> 0)
#define IMPROVE_IO() std::ios::sync_with_stdio(false)

using std::cin;
using std::cout;
using std::endl;

typedef long long int lli;

int getint() { int x; scanf("%d", &x); return x; }
lli getll() { long long int x; scanf("%lld", &x); return x; }

const int MAXN = 40000 + 10;

bool notprime[MAXN];
int prime[MAXN], phi[MAXN], cnt;
int n;
lli ans;

void Sieve() {
    notprime[0] = notprime[1] = true;
    phi[1] = 1;
    for (int i = 2; i < MAXN; ++i) {
        if (!notprime[i]) {
            prime[++cnt] = i; phi[i] = i - 1;
        }
        for (int j = 1; j <= cnt && (i * prime[j]) < MAXN; ++j) {
            int x = i * prime[j];
            notprime[x] = true;
            if (i % prime[j] == 0) { phi[x] = phi[i] * prime[j]; break; }
            phi[x] = phi[i] * (prime[j] - 1);
        }
    }
}

void Solve(int fn) {
    for (int x = 1; x <= fn; ++x) {
        ans += phi[x];
        if (x == 1) ans -= 1;
    }
}

int main() {
    Sieve();
    n = getint();
    if (n == 1) return (0 & printf("0\n"));
    Solve(n - 1);
    printf("%lld\n", ans * 2 + 3);
    return 0;
}