差分约束系统学习笔记

十月 17, 2020 3451

0x01 引子

解不等式组大家都会解吧
形式化地，给定一个不等式组

\left\{ \begin{array}{l} x_1 - x_2 \leq a\\ x_2 - x_3 \leq b\\ x_1 - x_3 \leq c \end{array} \right.

我们小学就学过加减消元：

\Rightarrow x_1 - x_3 \leq \min(a + b, c)

现在我们有这样一个结论。它有什么用呢？

0x02 将不等式放到图上

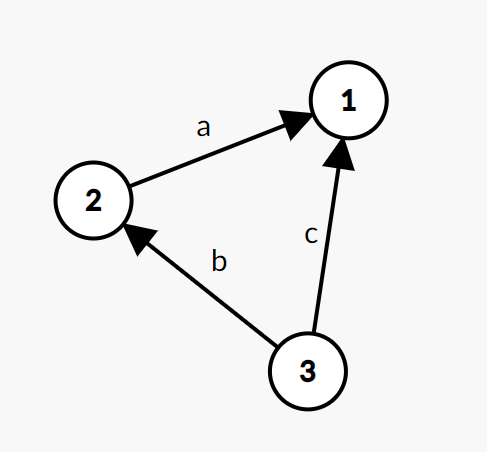
对于一个不等式 x_a - x_b \leq c ，我们在图上连一条 b \rightarrow a 权值为 c 的边，那么上面的不等式组就等价于：

很显然，我们发现 \min(a + b, c) 其实就是 3 到 1 的最短路

也即：不等式 x_1 - x_3 \leq k 的解集上下界等价于在图上跑最短路。

反过来也一样，不等式 x_1 - x_3 \geq k 的解集上下界等价于在图上跑最长路。

这个东西其实还有一个名字：三角形不等式。
这个东西将是我们后面确定跑最长路还是最短路的关键依据。

0x03 差分约束系统

所谓差分约束系统，就是给你 n 个变量组成 m 个系数为 \pm1 的不等式的系统。说人话就是一个不等式组

通过上面的例子可以看出，差分约束系统也等价于一个 n 个点 m 条边的有向带权图，在上面跑最短 / 长路就可以求出一些不等式的解集。

在一些限制类问题中，通过前缀和等方式可以把限制转化为不等式，进而组成不等式组，建立差分约束系统，从而高效地求解。

0x04 三角形不等式

通过运用三角形不等式，我们可以快速确定该跑最短路还是最长路。

例，有不等式组

\left\{ \begin{array}{l} x_1 - x_2 \geq c_1\\ x_2 - x_3 \geq c_2\\ x_3 - x_4 \geq c_3\\ \dots \end{array} \right.

只需要随便抽出三个合法的不等式：

\left\{ \begin{array}{l} x_1 - x_2 \geq c_1\\ x_2 - x_3 \geq c_2\\ x_1 - x_3 \geq c_k\\ \end{array} \right.

然后可以画出图：
0q8ZNj.png

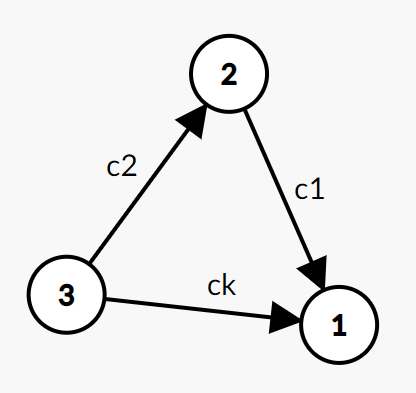
同时运用三角形不等式，

\Rightarrow x_1 - x_3 \geq \max(c_1 + c_2, c_k)

结合图可以看出，这相当于 2 \rightarrow 1 的最长路。也就是说，这道题需要跑最长路。

将这张图扩大到 n 个点 m 条边，就变成了一个 n 点 m 边的最长路问题。

0x04 一些比较特殊的不等号

差分约束系统的一般形式是 x_a - x_b \geq k 或 x_a - x_b \leq k 。但是做题的时候我们常常会碰见 >, <, \neq 甚至 = 这些符号，该怎么办呢？

  • 对于 a + b > c ，只要变量的取值在整数集里，我们完全可以把它转化成 a + b \geq c + 1 的形式；
  • 对于 a + b \neq c ，我们可以把它转化为 a + b > c 且 a + b < c ，再运用上一步转化大于小于号即可；
  • 对于 a + b = c ，我们可以把它转化为 c \leq a + b \leq c 的形式。

还有一种情况，就是 \leq, \geq 两个符号同时存在，这种情况也可以通过两边乘 -1 来使符号变换方向，从而统一不等式的符号。

0x05 解的存在性问题

01 不等式无解

不等式无解 \Leftrightarrow 图存在负环（最短路）或正环（最长路）

例：
不等式组

\left\{ \begin{array}{l} x_C - x_A \geq b\\ x_A - x_B \geq c\\ x_B - x_C \geq a\\ \dots \end{array} \right.

可转为一个最长路模型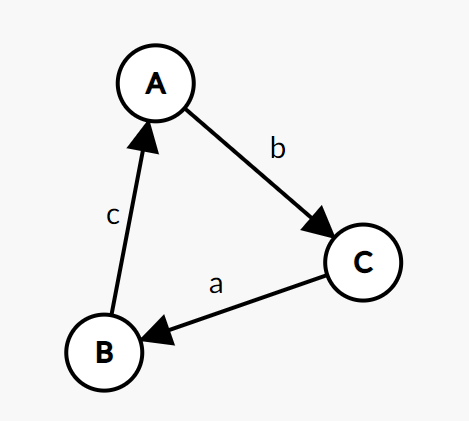
0q3Jpt.png
加减消元一下，会发现：

a + b + c \leq 0

所以当图跑最长路存在正环（即 a + b + c > 0 ）的时候，原不等式组无解。
反过来，对于最短路存在负环也是一样的。

10 不等式有无数解

例：

\left\{ \begin{array}{l} x_1 - x_2 \geq c_1\\ x_3 - x_4 \geq c_2\\ \end{array} \right.

图就不画了，显然这个图是不连通的。
同时可以发现 x_4 - x_1 最大值是无限大的，因为当 x_1 = x_2 + c_1, x_4 = x_3 - c_2 时，只要 x_2 足够小， x_3 足够大， x_4 - x_1 就可以足够大。

所以，当图跑最长路无法到达时，不等式的解无限大。反过来，跑最短路也是一样的。

0x06 例题

线性约束：3169 – Layout (poj.org)
题解点我

区间约束：1716 – Integer Intervals (poj.org)
题解点我

0x07 扩展阅读

讲得比我清晰多的博客，内含大量习题

也是一个非常好的文章

也可以来看看杂题选讲